Question

Volume of composite figures

Answer 1

Given:

The diameter of cylinder is 6 in and the height of the cylinder is 8 in.

The dimensions of the cuboid are 15 in by 9 in by 9 in.

To find:

The volume of the composite figure.

Solution:

Volume of a cuboid is:

`V_1=length* breadth* height`

`V_1=15* 9* 9`

`V_1=1215`

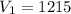
So, the volume of the cuboid is 1215 cubic inches.

The diameter of cylinder is 6 in. So, the radius of the cylinder is:

`(6)/(2)=3\text{ inches}`

Volume of a cylinder is:

`V_2=\pi r^2h`

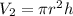
Where, r is the radius and h is the height.

Substituting
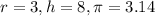`r=3,h=8,\pi =3.14`, we get

`V_2=(3.14)(3)^2(8)`

`V_2=(3.14)(9)(8)`

`V_2=226.08`

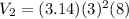
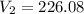
The volume of the cylinder is 226.08 cubic inches.

Now, the volume of the composite figure is:

`V=V_1+V_2`

`V=1215+226.08`

`V=1441.08`

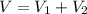
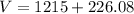
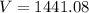
Therefore, the volume of the composite figure is 1441.08 cubic inches.