Given:
Principal = $1500
Time = 10 year
Amount after interest compounded continuously = $3935.36
To find:
The rate of interest.
Solution:
The formula for amount after continuous compound interest is:
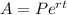
Where, P is principal, r is the rate of interest in decimal and t is time in years.
Putting
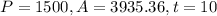 in the above formula, we get
in the above formula, we get
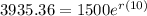
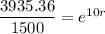

Taking ln on both sides, we get
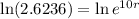
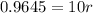
![[\because \ln e^x=x]](https://img.qammunity.org/2022/formulas/mathematics/high-school/m24tge2dslw94bp9jx3y240611r7x9yr3r.png)
Divide both sides by 10.

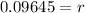
The rate of interest in percentage is:

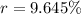
Therefore, the required rate of interest is 9.645%.