Question

Find x and y. give answer in insimplified radical form, not decimal.

Answer 1

Finding x,

We will use Pythagoras theorem to determine the value of x:

`9^(2) = {8}^(2) + {x}^(2) \\ 81 = 64 + {x}^(2) \\ 81 - 64 = {x}^(2) \\ {x}^(2) = 17 \\ x = √(17)`

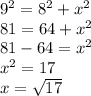
Finding y,

We have to determine the angle, at the bottom left of the bigger triangle.

Using sine rule,

`(9)/(sin(90)) = (8)/(sin(z)) \\ sin(z) = 0.8889 \\ z = {sin}^( - 1) (0.8889) \\ z = 62.73`

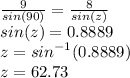
To find the angle on the smaller triangle,

`a = 90 - 62.73 \\ a = 27.27`

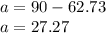
Finding the missing length of y,

`( √(17) )/(sin(62.73)) = (m)/(sin(27.27)) \\ m = 2`

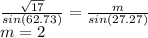
So y = 2 + 8, y = 10