Given:
In triangle XYZ, P is the centroid of triangle XYZ, YP = 8, QP = 5, YZ = 10.
To find:
The measure of median YS.
Solution:
We know that a centroid divides a median in 2:1.
P is the centroid and YS is the median. So,
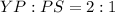
Let the measure of YP and PS are 2x and x.
It is given that the measure of YP is 8.
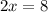
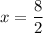
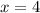
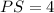
Now, the measure of YS is:
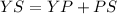
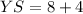
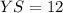
The measure of median YS is 12 units. Therefore, the correct option is (a).