Question

The focus of a parabola is (0, -3) and the directrix is y = 3. What is the equation of the parabola?

Answer 1

The equation of the parabola is
`y = -12\cdot x^(2)`.

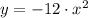Explanation:

Since the directrix is of the form
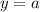`y = a`, the parabola is vertical. The vertex of the parabola (
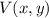`V(x,y)`) is the midpoint between the focus (
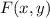`F(x,y)`) and a point of the directrix (
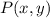`P(x,y)`), that is to say:

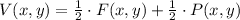`V(x,y) = (1)/(2)\cdot F(x,y) + (1)/(2)\cdot P(x,y)` (1)

If we know that
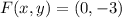`F(x,y) = (0, -3)` and
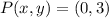`P(x,y) = (0, 3)`, then the coordinates of the vertex of the parabola:

`V(x,y) = (1)/(2)\cdot (0, -3) + (1)/(2)\cdot (0, 3)`

`V(x,y) = (0, 0)`

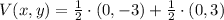
The vertex factor (
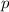`p`) is the distance of the focus with respect to the vertex:

`p = √([F(x,y)-V(x,y)]\,\bullet \,[F(x,y)-V(x,y)])` (2)

If we know that
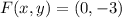`F(x,y) = (0, -3)` and
`V(x,y) = (0, 0)`, then the vertex factor is:

`p = \sqrt{0^(2)+(-3)^(2)}`

`p = -3`

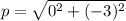
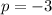
The equation of the parabola in the vertex form is described below:

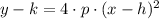`y - k = 4\cdot p \cdot (x-h)^(2)` (3)

Where:

`x` - Independent variable.

`y` - Dependent variable.

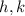`h, k` - Coordinates of the vertex.

If we know that
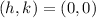`(h,k) = (0, 0)` and
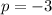`p = -3`, then the equation of the parabola is
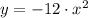`y = -12\cdot x^(2)`.