Given:
The geometric sequence is:
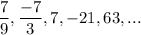
To find:
The 9th term of the given geometric sequence.
Solution:
We have,
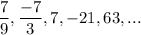
Here, the first term is:
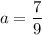
The common ratio is:
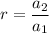
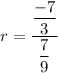
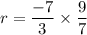
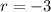
The nth term of a geometric sequence is:
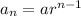
Where, a is the first term and r is the common ratio.
Substitute
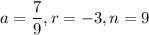 to find the 9th term.
to find the 9th term.
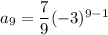
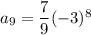
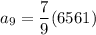
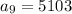
Therefore, the 9th term of the given geometric sequence is 5103.