Question

The mean high temperature on a particular day in January is 31 degrees F and the standard deviation is 8.7 degrees. One year, the temperature was 52 degrees F on that day. What is the Z-score for that day's temperature? Round to the appropriate number of decimal places for Z-scores. Is this temperature significantly high? (greater than 2)​

Answer 1

The Z-score for that day's temperature is 2.41, and since Z > 2, this temperature is significantly high.

Explanation:

Z-score:

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

If
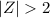`|Z| > 2`, the measure X is significantly high(Z > 2) or significantly low(Z < -2).

The mean high temperature on a particular day in January is 31 degrees F and the standard deviation is 8.7 degrees.

This means that
`\mu = 31, \sigma = 8.7`

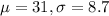
One year, the temperature was 52 degrees F on that day.

This means that
`X = 52`.

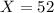What is the Z-score for that day's temperature?

`Z = (X - \mu)/(\sigma)`

`Z = (52 - 31)/(8.7)`

`Z = 2.41`

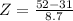
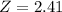
The Z-score for that day's temperature is 2.41, and since Z > 2, this temperature is significantly high.