Part 1
Answer: (x+5)(x+10) - 50 = 126
Other answers are possible.
-------------
Step-by-step explanation:
The old width was 5, but then it increases to x+5. The old length was 10, but now it's x+10.
The area of any rectangle is length times width.
So the area of the larger rectangle is (x+5)(x+10). Subtract off the old area of 5*10 = 50 and we get (x+5)(x+10) - 50 as the area of the L shape. Set this equal to 126 to finish setting up the equation. This is one possible answer out of many others. This is because we could expand out the (x+5)(x+10) into x^2+10x+5x+50 or simplify that to x^2+15x+50, as two possible options.
==========================================================
Part 2
Answer: x = 6
-------------
Step-by-step explanation:
Solve the equation we set up in the previous part
(x+5)(x+10) - 50 = 126
x^2+10x+5x+50-50 = 126
x^2+15x = 126
x^2+15x-126 = 0
Apply the quadratic formula from here
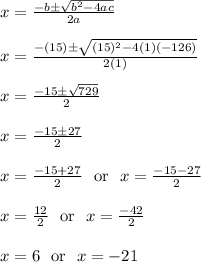
Another method you could use is factoring, so you could say:
x^2+15x-126 = 0
(x-6)(x+21) = 0
x-6 = 0 or x+21 = 0
x = 6 or x = -21
The issue with this is that it may take a while to do this trial and error approach.
Whichever method you used, you'll end up with two solutions. One of those solutions doesn't make sense though. We can't have a negative length or distance value, so we ignore x = -21.
The only practical solution is x = 6
If x = 6, then the old height goes from 5 to x+5 = 6+5 = 11
If x = 6, then the old length goes from 10 to x+10 = 6+10 = 16
The new larger rectangle is 11*16 = 176 sq ft, in which we subtract off the 50 sq ft to get 176-50 = 126 sq ft, and this matches with the 126 given to us. Therefore, the answer is confirmed.