2 Answers

Ask a Question

Chris Newman · Answer 1 · 2022-04-22T14:27:07+0000

Answer:

$\boxed {\boxed {\sf 24 \ inches}}}$

Explanation:

We want to find the diameter of the tire given the distance traveled in 1 full rotation.

The circumference of a circle is the distance all the way around. If a wheel or tire makes 1 full rotation, the distance traveled is equal to the circumference.

The circumference is the product of pi and the diameter.

$c=\pi * d$

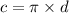
We know the circumference (distance traveled in 1 full rotation) is 75 inches. We can substitute this value for c.

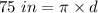
$75 \ in =\pi * d$

We want to find the diameter, so the variable must be isolated. It is being multiplied by pi. The inverse of multiplication is division, so we divide both sides by pi.

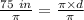
$\frac {75 \ in}{\pi}= (\pi * d)/(\pi)$

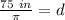
$\frac {75 \ in}{\pi}=d$

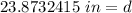
$23.8732415 \ in=d$

Round to the nearest inch. The 8 in the tenths place tells us to round the 3 up to a 4.

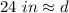
$24 \ in \approx d$

The diameter of the tire is approximately 24 inches.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

2 Answers

24 inches

0 Comments

Please log in or register to add a comment.

0 Comments

Please log in or register to add a comment.

Other Questions