Answer:
1. --a 10
--b 100 in.
2. --a 4
--b 4
3. --a 2
--b 30 rpm
--c 75 ft.·lb.
4. --a Second class lever
--b 50 lbs.
Step-by-step explanation:
The Actual Mechanical Advantage, AMA, is given as follows;
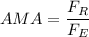
Where;
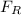 = The resistance force magnitude
= The resistance force magnitude
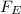 = The effort force magnitude
= The effort force magnitude
1. a. We have;
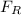 = 10 lb.
= 10 lb.
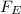 = 100 lb.
= 100 lb.

b.

The diameter of the axle, d = 2 in.
Let 'D' represent the diameter of the wheel, we have;
The distance moved by the axle, c = π·d
The distance moved by the load, C = π·D

∴ 2 × 10 = D
D = 20 in.
The required wheel diameter to overcome the resistance force, D = 100 in.
2. --a The mass of the participants, m = 200 lb.
The depth of the ground of the participants = 20 feet
The effort force = 50 lb
Actual Mechanical Advantage, AMA = 200 lb./(50 lb.) = 4
--b. The number of strands of pulley needed ≈ The mechanical advantage = 4
3. The number of gears on Gear A = 10 teeth
The number of gears on Gear B = 8 teeth
The number of gears on Gear C = 20 teeth
-a. Given that the driver gear = Gear A
The output gear = Gear C
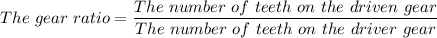
The driver gear = The input gear
Therefore, we have;

The gear ratio = 2
-b
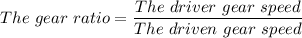
Therefore, we have;
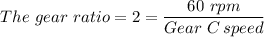
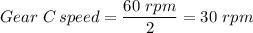
-c The output (driven) gear torque at Gear C = 150 ft.·lb.
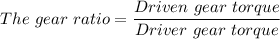
Therefore;
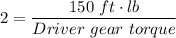
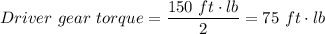
The input (driver) torque at Gear A = 75 ft·lb
4. -a Given that the load is between the effort and the fulcrum, we have;
The type of lever is a second class lever
-b The distance between the load and the fulcrum = 4 feet
The distance between the effort and the fulcrum = 8 feet
We have;
100 lbs × 4 ft. = Effort × 8 ft.
∴ Effort = 100 lbs × 4 ft./(8 ft.) = 50 lbs.
The effort = 50 lbs.