Question

The movement of moving particles is described in the equation r=ht22 −2vt−2c. Solve the equation for v.

Pls help

Answer 1

`v=(r-ht^2+2c)/(-2t)`

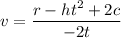
Explanation:

The given equation is :

`r=ht^2 -2vt-2c`

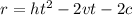
We need to solve the above equation for v.

Subtract ht² from both sides.

r-ht²= ht²-2vt-2c-ht²

r-ht² = -2vt-2c

Adding 2c both sides,

r-ht² +2c= -2vt-2c+2c

r-ht² +2c = -2vt

Dividing both sides by (-2t)

`v=(r-ht^2+2c)/(-2t)`

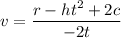
So, the value of v is equal to
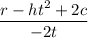`(r-ht^2+2c)/(-2t)`.