Answer:
? = 9.2
Explanation:
The angle between a tangent and radius at the point of contact is 90°
Then the triangle shown is right with legs ? , 6.9 and hypotenuse = (6.9 + 4.2) = 11.5
Using Pythagoras' identity in the right triangle
?² + 6.9² = 11.5²
?² + 47.61 = 132.25 ( subtract 47.61 from both sides )
?² = 84.64 ( take the square root of both sides )
? =
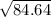 = 9.2
= 9.2