Question

The graph at the right shows

a function, f, graphed on the
domain 0 < x < 8.
The section from A to B is a
straight segment.
The section from B to C is
represented by y = (x - 5)^2

1. Find the slope of the segment from A to B.

2. Find the x-coordinate of the relative minimum
value of the graph from B to C.

3. Find the value of f (3) + f (4) + f (6) + f (7).

Answer 1

Explanation:

1). Since, line segment AB passes through two points ((0, 0) and (3, 4)

Therefore, slope of the segment =
`(y_2-y_1)/(x_2-x_1)`

=
`(4-0)/(3-0)`

=
`(4)/(3)`

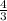
2). Relative minimum of the graph from B to C → (5, 0)

Therefore, x-coordinate of the relative minimum → x = 5

3). From the graph attached,

f(3) = 4

f(4) = 1

f(6) = 1

f(7) = 4

Therefore, f(3) + f(4) + f(6) + f(7) = 4 + 1 + 1 + 4

= 10