Answer:
![[I_2]=[Br]=0.31M](https://img.qammunity.org/2022/formulas/chemistry/college/v1c4fboytq9irsgedb6oig6xk5e2koo2hp.png)
Step-by-step explanation:
Hello there!
In this case, according to the given information, it is possible for us to set up the following chemical equation at equilibrium:
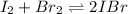
Now, we can set up the equilibrium expression in terms of x (reaction extent) whereas the initial concentration of both iodine and bromine is 0.5mol/0.250L=2.0M:
![K=([IBr]^2)/([I_2][Br_2]) \\\\1.2x10^2=((2x)^2)/((2.0-x)^2)](https://img.qammunity.org/2022/formulas/chemistry/college/32km4as4u78ieswgl1xq5gxkbv110u291h.png)
Thus, we solve for x as show below:
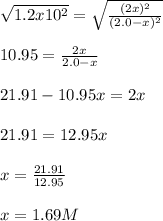
Therefore, the concentrations of both bromine and iodine are:
![[I_2]=[Br]=2.0M-1.69M=0.31M](https://img.qammunity.org/2022/formulas/chemistry/college/nlbqw44jcync7h81y7bg9byzb7u5tehhfr.png)
Regards!