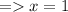Question

USE LAWS OF EXPONENT TO FIND THE VALUE OF X
㏒ ₆₄ 8=X÷2

Answer 1

x = 1

Explanation:

FACTS TO KNOW BEFORE SOLVING :-

Lets say , there's an expression →
`a = b^c`

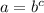
In terms of logarithm , it can be written as →
`\log_b a = c`

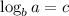
SOLUTION :-

`\log_(64)8 = (x)/(2)`

It can be also written as -

`64^{(x)/(2) }= 8`

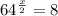
In L.H.S. , 64 can be written as 8² and in R.H.S. , 8 can be written as 8¹. So,

`=> 8^{((x)/(2) * 2)} = 8^1`

`=> 8^x = 8^1`

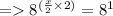
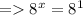
According to the law of exponents , the bases are equal in L.H.S & R.H.S. .So, their exponents in L.H.S. & R.H.S. must be equal.

`=> x = 1`