Given:
The width at the base of parabolic tunnel is 7 m.
The ceiling 3 m from each end of the base there are light fixtures.
The height to light fixtures is 4 m.
To find:
Whether it is possible a trailer truck carrying cars is 4 m wide and 2.8 m high is going to drive through the tunnel.
Solution:
The width at the base of tunnel is 7 m.
Let the graph of the parabola intersect the x-axis at x=0 and x=7. It means x and (x-7) are the factors of the height function.
The function of height is:
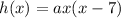 ...(i)
...(i)
Where, a is a constant.
The ceiling 3 m from each end of the base there are light fixtures and the height to light fixtures is 4 m. It means the graph of height function passes through the point (3,4).
Putting x=3 and h(x)=4 in (i), we get

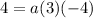
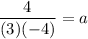
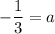
Putting
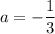 , we get
, we get
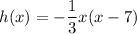 ...(ii)
...(ii)
The center of the parabola is the midpoint of 0 and 7, i.e., 3.
The width of the truck is 4 m. If is passes through the center then the truck must m 2 m on the left side of the center and 2 m on the right side of the center.
2 m on the left side of the center is x=1.5.
A trailer truck carrying cars is 4 m wide and 2.8 m high is going to drive through the tunnel is possible if h(1.5) is greater than 2.8.
Putting x=1.5 in (ii), we get
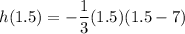
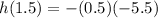
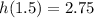
Since h(1.5)<2.8, therefore the trailer truck carrying cars is 4 m wide and 2.8 m high is going to drive through the tunnel is not possible.