Question

What is the perimeter of parallelogram RSTU, rounded to the nearest whole number? ​

Answer 1

Given:

The vertices of the parallelogram RSTU are R(-4,4), S(2,6), T(6,2) and U(0,0).

To find:

The perimeter of parallelogram RSTU, rounded to the nearest whole number.

Solution:

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

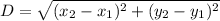
Using the distance formula, we get

`RS=√((2-(-4))^2+(6-4)^2)`

`RS=√((6)^2+(2)^2)`

`RS=√(36+4)`

`RS=√(40)`

`RS=6.32`

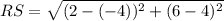
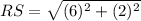
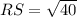
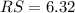
Similarly,

`ST=√(\left(6-2\right)^2+\left(2-6\right)^2)`

`ST\approx 5.66`

`TU=√(\left(0-6\right)^2+\left(0-2\right)^2)`

`TU\approx 6.32`

`RU=√(\left(0-\left(-4\right)\right)^2+\left(0-4\right)^2)`

`RU\approx 5.66`

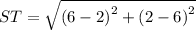
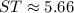
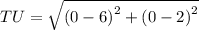
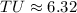
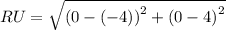
Now, the perimeter of the parabola is:

`P=RS+ST+TU+RU`

`P=6.32+5.66+6.32+5.66`

`P=23.96`

`P\approx 24`

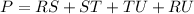
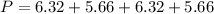
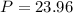
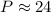
The perimeter of the parallelogram RSTU is 24 units.

Therefore, the correct option is C.

Note: Unit of perimeter cannot be in square.