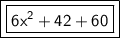
In the standard form, we will have:
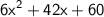
Development
We have the function:
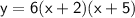
First, we must multiply the terms that are in parentheses. Applying distributive property.
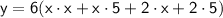
We will perform the multiplication.
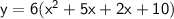
We will perform the indicated operation.
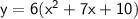
Now, we can multiply the number 6 by what is in parentheses. Also applying distributive property.
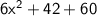
Conclusion
The answer of this function is: