Answer:
The angular velocity of the tennis ball is 10 radians per second.
Explanation:
The tennis ball can be represented as a particle, the angular momentum (
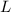 ), in kilogram-square meter per second, of the tennis ball is described by the following formula:
), in kilogram-square meter per second, of the tennis ball is described by the following formula:
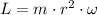 (1)
(1)
Where:
 - Mass of the tennis ball, in kilograms.
- Mass of the tennis ball, in kilograms.
 - Radius of gyration, in meters.
- Radius of gyration, in meters.
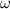 - Angular velocity, in radians per second.
- Angular velocity, in radians per second.
If we know that
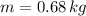 ,
,
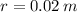 and
and
 , then the angular velocity of the tennis ball is:
, then the angular velocity of the tennis ball is:
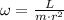
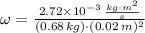
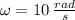
The angular velocity of the tennis ball is 10 radians per second.