Answer:
Solution given:
Y=90°
∠X=73°.
∠ZWY=80°
and XW=80.
ZY=?
We know that
In right angled triangle ∆ XYZ
Tan 73=
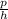
3.27=
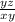
3.27×[xy]=yz
xw+wy=
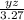
wy=
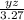 -80...........(1)
-80...........(1)
again
In right angled triangle WYZ
Tan 80=

5.67×wy=yz
wy=
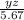
yz=5.67×wy............................................(2)
Equating equation 1&2
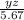 =
=
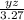 -80
-80
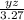 -
-
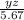 =80
=80
5.67yz-3.27yz=80*5.67*3.27
2.4yz =1483.272
yz=
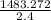
yz=618.03
:.y=618.03unit.the length of ZY to the nearest 100th is 618.