Question

If the area of AABC is D, give the expressions that complete the equation for the measure of ZB?

m m=
n =

Answer 1

Given:

The figure of triangle ABC.

The area of the triangle ABC is D.

`m\angle B=\sin ^(-1)((m)/(n))`

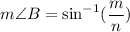
To find:

The value of m and n in the given expression.

Solution:

Let h be the height of the triangle ABC.

Area of a triangle is:

`Area=(1)/(2)* base* h`

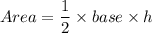
Where, b is the base and h is the height of the triangle.

`Area=(1)/(2)* a* h`

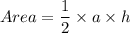
The area of the triangle ABC is D.

`D=(1)/(2)* a* h`

`2D=ah`

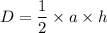
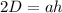
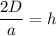`(2D)/(a)=h` ...(i)

In a right angle triangle,

`\sin \theta =(Perpendicular)/(Hypotenuse)`

`\sin B =(h)/(c)`

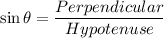
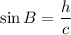
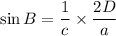`\sin B =(1)/(c)* (2D)/(a)` [Using (i)]

`\sin B =(2D)/(ac)`

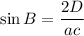
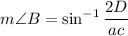`m\angle B =\sin ^(-1)(2D)/(ac)` ...(ii)

We have,

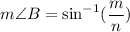`m\angle B=\sin ^(-1)((m)/(n))` ...(iii)

On comparing (ii) and (iii), we get

`m=2D`

`n=ac`

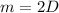
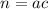
Therefore, the required values are
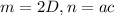`m=2D, n=ac`.