Answer:
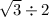
Explanation:
there are multiple ways to get to the result. and it took me a little while to figure out your symbolic. I am not sure about the context of your problem, so I try to give you 2 ways.
1. similar triangles.
they have the same angles, and therefore the change factor for their side lengths (to change from one similar triangle to the other) must be the same for all sides.
tan of an angle is the length of the outside tangent touching the circle starting at x=1,y=0 and going up perpendicular all the way until it crosses the line from the center of the circle enclosing the angle.
so, we have one triangle of the corners ABC, where A=(0,0), B=(1,0), C=(1,tan of the angle = sqrt(3)).
and we have a similar triangle ADE, where A=(0,0), D=(cos of the angle=1/2,0), E=(1/2,m).
we know because of the described similarity that the sides BC and DE must have the same ratio as e.g. AB and AD.
AB=1, AD=1/2, so the ratio AD/AB = 1/2.
now, BC=sqrt(3). DE=m and must follow the same ratio as AD/AB. DE/BC=1/2.
=> m/sqrt(3)=1/2 => m=sqrt(3)/2
2. circle equation : x^2 + y^2=r^2
x=1/2, y=m, r=1
(1/2)^2 + m^2 = 1^2 (= 1)
1/4 + m^2 = 1
m^2 = 3/4
m = sqrt(3)/sqrt(4) = sqrt(3)/2