Answer:
P(25 < x < 37) = 0.77
Explanation:
Given - If a Variable has a normal distribution with mean 30 and standard deviation 5
To find - find the probability that the variable will be between 25 and 37.
Proof -
Given that,
Mean, μ = 30
S.D, σ = 5
Now,
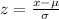 ~ N(0,1)
~ N(0,1)
Now,
P(25 < x < 37)
=
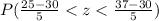
= P(1 < z < 1.4)
= P(z < 1.4) - P(z < -1)
= 0.9192 - 0.1587
= 0.7605
≈ 0.77
∴ we get
P(25 < x < 37) = 0.77