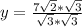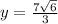Answer:
A.
![x = \frac{7√(6){3}]()
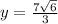
Explanation:
Reference angle = 60°
Opposite =
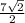
Hypotenuse = x
Adjacent = y
✔️To find x, apply the trigonometric function SOH:
Sin 60° = Opp/Hyp
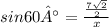
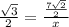 (sin 60 = √3/2)
(sin 60 = √3/2)
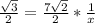
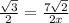
Cross multiply
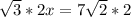
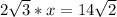
Divide both sides by 2
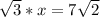
Divide both sides by √3
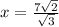
Rationalize
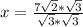
![x = \frac{7√(6){3}]()
✔️To find y, apply the trigonometric function TOA:
Tan 60° = Opp/Adjacent
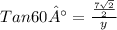
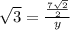 (tan 60 = √3)
(tan 60 = √3)
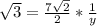
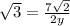
Cross multiply
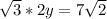
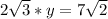
Divide both sides by √3
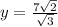
Rationalize