Question

The length of a rectangle is 5 metres less than twice the breadth. If the perimeter is 50 meters,find the length and breadth

Answer 1

S O L U T I O N :

As per the given question, it is stated that the length of a rectangle is 5 m less than twice the breadth.

Assumption : Let us assume the length as "l" and width as "b". So,

`\twoheadrightarrow \quad\sf{ Length =2(Width)-5}`

`\twoheadrightarrow \quad\sf{ \ell=(2b-5) \; m}`

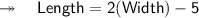
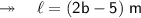
Also, we are given that the perimeter of the rectangle is 50 m. Basically, we need to apply here the formula of perimeter of rectangle which will act as a linear equation here.

`\\ \twoheadrightarrow \quad\sf{ Perimeter_((Rectangle)) = 2(\ell +b) } \\`

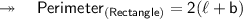
• l denotes length
• b denotes breadth

`\\ \twoheadrightarrow \quad\sf{50= 2(2b-5+b)} \\`

`\\ \twoheadrightarrow \quad\sf{50= 2(3b-5)} \\`

`\\ \twoheadrightarrow \quad\sf{50= 6b - 10} \\`

`\\ \twoheadrightarrow \quad\sf{50+10= 6b} \\`

`\\ \twoheadrightarrow \quad\sf{60= 6b} \\`

`\\ \twoheadrightarrow \quad\sf{\cancel{(60)/(6)}=b} \\`

`\\ \twoheadrightarrow \quad\underline{\bf{10\; m = Width }} \\`

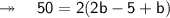
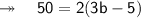
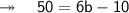
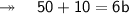
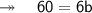
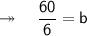
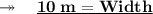
Now, finding the length. According to the question,

`\twoheadrightarrow \quad\sf{ \ell=(2b-5) \; m}`

`\twoheadrightarrow \quad\sf{ \ell=2(10)-5\; m}`

`\twoheadrightarrow \quad\sf{ \ell=20-5\; m}`

`\\ \twoheadrightarrow \quad\underline{\bf{15\; m = Length }} \\`

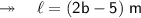
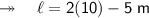
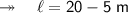
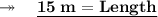
Therefore, length and breadth of the rectangle is 15 m and 10 m.