Answer:
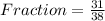
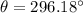
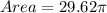
Explanation:
Given
 --- radius
--- radius
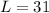 --- arc length
--- arc length
Solving (a): Fraction represented by the arc
First, calculate the circumference (C)

So, we have:
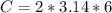
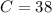 --- approximated
--- approximated
So, the fraction represented by the arc is:

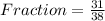
Solving (b): Measure of the center angle
Using arc length formula, we have:
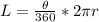
This gives
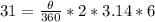
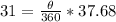
Make
 the subject
the subject
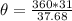
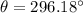
Solving (c): The area of the sector
This is calculated as:

So, we have:
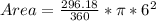
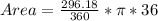
Divide 360 and 36
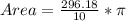

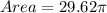 --- approximated
--- approximated