Question

Find the radius of convergence and the interval of convergence.


`\displaystyle \sum \limit_(n=1)^\infty \frac{x^\text{n}}{2^\text{n}(n+1)^2}`

Answer 1

Radius of Convergence: 2

Interval of Convergence: [-2, 2]

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Exponential Rule [Multiplying]:
  `\displaystyle b^m \cdot b^n = b^(m + n)`
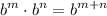
• Exponential Rule [Dividing]:
  `\displaystyle (b^m)/(b^n) = b^(m - n)`

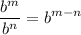
Calculus

Series Convergence Tests

• P-Series:
  `\displaystyle \sum \limit_(n = 1)^\infty (1)/(n^p)`
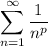
• Direct Comparison Test (DCT)
• Alternating Series Test (AST)
• Ratio Test:
  `\displaystyle \lim_(n \to \infty) \bigg| (a_(n + 1))/(a_n) \bigg|`

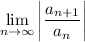
Radius of Convergence (ROC)

• Ratio Test
• Interval bound

Interval of Convergence (IOC)

• Testing endpoints

Explanation:

Step 1: Define

`\displaystyle \sum \limit_(n = 1)^\infty (x^n)/(2^n(n + 1)^2)`

Step 2: Find ROC

Apply Ratio Test

1. [Series] Set up [Ratio Test]:
   `\displaystyle \lim_(n \to \infty) \bigg|(x^(n + 1))/(2^(n + 1)(n + 2)^2) \cdot (2^n(n + 1)^2)/(x^n) \bigg|`
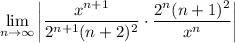
2. [Ratio Test] Rewrite exponentials [Exponential Rule - Multiplying]:
   `\displaystyle \lim_(n \to \infty) \bigg|(x^n \cdot x)/(2^n \cdot 2(n + 2)^2) \cdot (2^n(n + 1)^2)/(x^n) \bigg|`
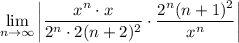
3. [Ratio Test] Simplify:
   `\displaystyle \lim_(n \to \infty) \bigg| (x)/(2(n + 2)^2) \cdot (n + 1)^2 \bigg|`
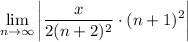
4. [Ratio Test] Multiply:
   `\displaystyle \lim_(n \to \infty) \bigg| (x(n + 1)^2)/(2(n + 2)^2) \bigg|`
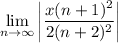
5. [Ratio Test] Evaluate limit:
   `\displaystyle \bigg| (x)/(2) \bigg| < 1`
6. [Ratio Test] Isolate x:
   `\displaystyle |x| < 2`

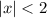
Our ROC is 2.

Step 3: Find IOC

Test endpoints

1. [ROC] Find interval bound:
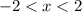
   `\displaystyle -2 < x < 2`

x = -2

1. Substitute in x [Series]:
   `\displaystyle \sum \limit_(n = 1)^\infty ((-2)^n)/(2^n(n + 1)^2)`
2. [Series] Rewrite [Exponential Rules - Multiplying]:
   `\displaystyle \sum \limit_(n = 1)^\infty ((-1)^n2^n)/(2^n(n + 1)^2)`
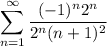
3. [Series] Simplify:
   `\displaystyle \sum \limit_(n = 1)^\infty ((-1)^n)/((n + 1)^2)`

Test convergence of modified series: Alternating Series Test

1. [AST] Condition 1 [Limit Test]:
   `\displaystyle \lim_(n \to \infty) (1)/((n + 1)^2) = 0 \ \checkmark`
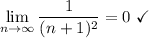
2. [AST] Condition 2 [aₙ vs bₙ comparison]:
   `\displaystyle (1)/((n + 2)^2) \le (1)/((n + 1)^2) \ \checkmark`

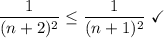
At x = -2, the series is convergent.

∴ Current IOC is -2 ≤ x < 2 or [-2, 2); 2 undetermined

x = 2

1. Substitute in x [Series]:
   `\displaystyle \sum \limit_(n = 1)^\infty (2^n)/(2^n(n + 1)^2)`
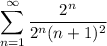
2. [Series] Simplify:
   `\displaystyle \sum \limit_(n = 1)^\infty (1)/((n + 1)^2)`

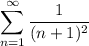
Test convergence of modified series: Direct Comparison Test

1. [DCT] Condition 1 [Define comparing series]:
   `\displaystyle \sum \limit_(n = 1)^\infty (1)/(n^2)`
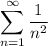
2. [DCT] Condition 1 [Test convergence of comparing series]:
   `\displaystyle p = 2 > 1, \ \sum \limit_(n = 1)^\infty (1)/(n^2) \ \text{convergent by p-series}`
3. [DCT] Condition 2 [aₙ vs bₙ comparison]:
   `\displaystyle (1)/((n + 1)^2) \le (1)/(n^2) \ \checkmark`

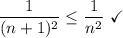
At x = 2, the series is convergent.

∴ IOC for
`\displaystyle \sum \limit_(n = 1)^\infty (x^n)/(2^n(n + 1)^2)` is -2 ≤ x ≤ 2 or [-2, 2]

Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Taylor Polynomials and Approximations - Power Series (BC Only)

Book: College Calculus 10e