Question

What is an equation of the line that passes through the points (4, -1) and
(-8. – 7)?

Answer 1

`y = (1)/(2) x - 3`

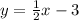
Explanation:

The equation of a line can be written in the form of y=mx +c, where m is the gradient and c is the y-intercept.

`\boxed{gradient = (y1 - y2)/(x1 - x2) }`

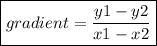
Using the gradient formula above,

gradient of line

`= ( - 1 - ( - 7))/(4 - ( - 8))`

`= ( - 1 + 7)/(4 + 8)`

`= (6)/(12)`

`= (1)/(2)`

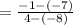
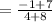
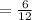
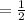
Substitute m= ½ into the equation:

y= ½x +c

To find the value of c, substitute a pair of coordinates.

When x= 4, y= -1,

`- 1 = (1)/(2) (4) + c`

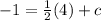
-1= 2 +c

c= -1 -2 (-2 on both sides)

c= -3

∴ The equation of the line is y= ½x -3.