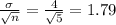Question

A small school with 60 total students records how many of their students attend school on each of the 180

days in a school year. The mean number of students in attendance daily is 55 students and the standard
deviation is 4 students. Suppose that we take random samples of 5 school days and calculate the mean
number of students ĉ in attendance on those days in each sample.
Calculate the mean and standard deviation of the sampling distribution of

Answer 1

The answer is below

Step-by-step explanation:

Given that the mean of the attendance of the population (μ) = 55 students, and the standard deviation (σ) = 55 students

If repeated random samples of a given size n are taken from a population with a population mean of μ and the population standard deviation of σ, then the mean of the sample distribution (
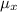`\mu_x`) is population mean μ, while the standard deviation of the sample distribution (
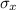`\sigma_x`) is the population standard deviation divided by the square root of the sample size.

Given a random sample (n) of 5 days, hence:

mean of sampling distribution (
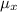`\mu_x`) = μ = 55 students

standard deviation of the sampling distribution =
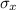`\sigma_x` =
`(\sigma)/(√(n) )=(4)/(√(5) ) =1.79`