Question

Claire invested $2,400 in an account paying an interest rate of 3.5% compounded monthly. Assuming no deposits or withdrawals are made, how long would it take, to the nearest year, for the value of the account to reach $4,490?

Answer 1

18 years (to the nearest year)

Explanation:

Compound interest formula:

`A=P(1+(r)/(n))^(nt)`

where A is amount, P is principal, r is interest rate (decimal format), n is the number of times interest is compounded per unit 't', and t is time

Given:

• A = 4490
• P = 2400
• r = 3.5% = 0.035
• n = 12

`\implies 4490=2400(1+(0.035)/(12))^(12t)`

`\implies (449)/(240)=\left((2407)/(2400)\right)^(12t)`

`\implies \ln(449)/(240)=\ln\left((2407)/(2400)\right)^(12t)`

`\implies \ln(449)/(240)=12t\ln\left((2407)/(2400)\right)`

`\implies t=(\ln(449)/(240))/(12\ln\left((2407)/(2400)\right))`

`\implies t=17.92277136...`

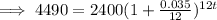
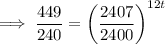
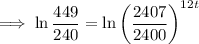
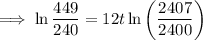
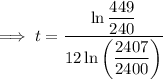
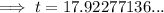
Therefore, it would take 18 years (to the nearest year) for the account to reach $4,490