Question

g PRACTICE ANOTHER Two trains approach each other on separate but adjacent tracks. Train 1 is traveling at a speed of 30.3 m/s and train 2 at a speed of 22.5 m/s. If the engineer of train 1 sounds his horn which has a frequency of 520 Hz, determine the frequency of the sound heard by the engineer of train 2. (Use 343 m/s as the speed of sound. Enter your answer to the nearest Hz.)

Answer 1

f'= 607.8 Hz

Step-by-step explanation:

This is a Doppler effect exercise due to the relative velocity of the sound source and the observer.

By the time the source and the observer are getting closer the expression is

f ’=
`f_o \ ( v+ v_o)/(v - v_s)`

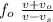
where vs is the speed of the source, vo is the speed of the observer, if the bodies move away the signs are exchanged

in this case, train 1 emits sound, so its speed is v_s = 30.3 m / s and train 2 is the receiver of the sound v₀ = 22.5 m / s

let's calculate

f ’=
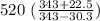`520 \ ( (343 + 22.5)/(343 - 30.3) )`520 (343+ 22.5 / 343 - 30.3)

f'= 607.8 Hz