Question

100 points to who ever can answer this the best

Answer 1

a. n =17

b. n =23

c. n = 9

d. n = 15

Answer 2

(a) n = 17

(b) n = 23

(c) n = 9

(d) n = 15

Explanation:

Sum of the first n terms of an arithmetic series:

`\boxed{S_n=(n)/(2)(a+a_n)}`

where:

• a is the first term.
• aₙ is the nth term.

Part (a)

`\displaystyle \sum^n_(i=1)(3i+5)=544`

To find a substitute i = 1 into the equation:

`\implies a=3(1)+5=8`

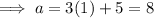
To find aₙ substitute i = n into the equation:

`\implies a_n=3n+5`

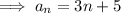
Substitute the values of a, aₙ and Sₙ into the arithmetic series formula and solve for n:

`\begin{aligned}S_n & =(n)/(2)(a+a_n)\\ \implies 544&=(n)/(2)(8+3n+5)\\1088&=n(3n+13)\\1088&=3n^2+13n\\3n^2+13n-1088&=0\\3n^2-51n+64n-1088&=0\\3n(n-17)+64(n-17)&=0\\(n-17)(3n+64)&=0\\\\n-17&=0 \implies n=17\\3n+64&=0 \implies n=-(64)/(3) \end{aligned}`

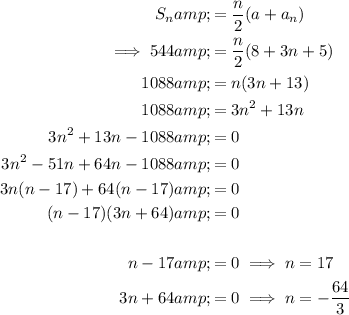
As n is positive, n = 17.

Part (b)

`\displaystyle \sum^n_(i=1)(-4i-1)=-1127`

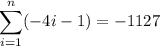
To find a substitute i = 1 into the equation:

`\implies a=-4(1)-1=-5`

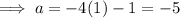
To find aₙ substitute i = n into the equation:

`\implies a_n=-4n-1`

Substitute the values of a, aₙ and Sₙ into the arithmetic series formula and solve for n:

`\begin{aligned}S_n & =(n)/(2)(a+a_n)\\ \implies -1127&=(n)/(2)(-5-4n-1)\\-2254&=n(-4n-6)\\-2254&=-4n^2-6n\\4n^2+6n-2254&=0\\2n^2+3n-1127&=0\\2n^2-46n+49n-1127&=0\\2n(n-23)+49(n-23)&=0\\(2n+49)(n-23)&=0\\\\2n+49&=0 \implies n=-(49)/(2)\\n-23&=0 \implies n=23 \end{aligned}`

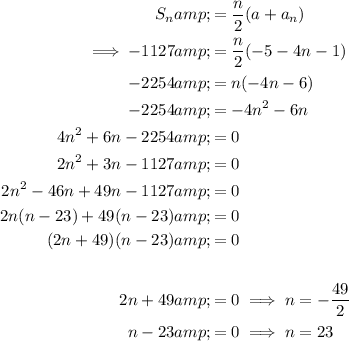
As n is positive, n = 23.

Part (c)

`\displaystyle \sum^n_(i=5)(7+12i)=455`

`\boxed{\displaystyle \sum _(i=m)^n\:=\:\sum _(i=1)^n\:-\:\sum _(i=1)^(m-1)}`

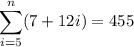
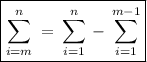
Therefore:

`\displaystyle \sum^n_(i=1)(7+12i)-\sum^(4)_(i=1)(7+12i)=455`

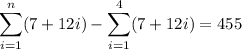
To find a substitute i = 1 into the equation:

`\implies a=7+12(1)=19`

To find aₙ substitute i = n into the equation:

`\implies a_n=7+12n`

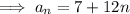
To find a₄ substitute i = 4 into the equation:

`\implies a=7+12(4)=55`

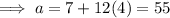
Therefore:

`\begin{aligned}\displaystyle \sum^n_(i=1)(7+12i)-\sum^(4)_(i=1)(7+12i)&=455\\(n)/(2)(19+7+12n)-(4)/(2)(19+55)&=455\\(n)/(2)(12n+26)-148&=455\\ (n)/(2)(12n+26)&=603\\6n^2+13n&=603\\6n^2+13n-603&=0\\ 6n^2-54n+67n-603&=0\\6n(n-9)+67(n-9)&=0\\(6n+67)(n-9)&=0\\\\6n+67&=0 \implies n=-(67)/(6)\\n-9&=0 \implies n=9\end{aligned}`

As n is positive, n = 9.

Part (d)

`\displaystyle \sum^n_(i=3)(-3-4i)=-507`

`\boxed{\displaystyle \sum _(i=m)^n\:=\:\sum _(i=1)^n\:-\:\sum _(i=1)^(m-1)}`

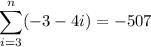
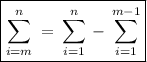
Therefore:

`\displaystyle \sum^n_(i=1)(-3-4i)-\sum^(2)_(i=1)(-3-4i)=-507`

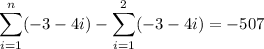
To find a substitute i = 1 into the equation:

`\implies a=-3-4(1)=-7`

To find aₙ substitute i = n into the equation:

`\implies a_n=-3-4n`

To find a₂ substitute i = 2 into the equation:

`\implies a=-3-4(2)=-11`

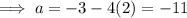
Therefore:

`\begin{aligned}\displaystyle \sum^n_(i=1)(-3-4i)-\sum^(2)_(i=1)(-3-4i)&=-507\\(n)/(2)(-7-3-4n)-(2)/(2)(-7-11)&=-507\\(n)/(2)(-4n-10)+18&=-507\\-2n^2-5n&=-525\\2n^2+5n-525&=0\\ 2n^2-30n+35n-525&=0\\2n(n-15)+35(n-15)&=0\\(2n+35)(n-15)&=0\\\\2n+35&=0 \implies n=-(35)/(2)\\n-15&=0 \implies n=15 \end{aligned}`

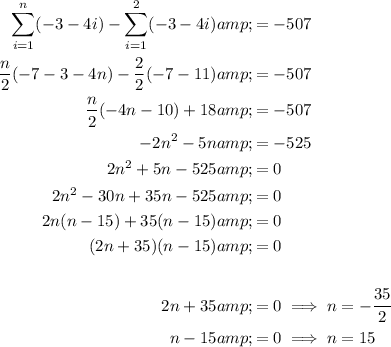
As n is positive, n = 15.