Answer:
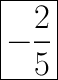
Explanation:
The slope of a line can be determined from two points via the slope formula. This is usually defined as the change in y divided by the change in x. It’s commonly represented using this formula:
Where
 represents “change in.”
represents “change in.”
The slope is basically just saying the rate of increase/decrease a function has when x increases by 1 - how much does y change when x increases by 1? We can find this by taking larger values and dividing by the rate at which we took the larger values. This derives the slope formula.
We can find the change in y and x in this function by analyzing the two points given. If we look at the change between each point, we can get the change since this is a line and thus has a constant slope.
- The change in y will be 12. This is because from -2 to 10 is 10 units -
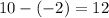
- The change in x will be -30. This is because from 19 to -11 is -30 units -
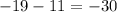
Now that we have our change in x and y, we can substitute these values into the slope formula.
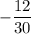
- Simplify - divide numerator and denominator by 6
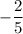
Therefore, the slope of this line is
 .
.
Hope this helped!