Question

PLEASE HELP ME mhanifa
​

Answer 1

Explanation:

10). m(arc AB) = m(arc BC) = m(arc CA) [given in the picture]

m(arc AB) =
`(360^0)/(3)`

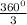
= 120°

Therefore, m(arc ACB) = m(arc AC) + m(arc BC)

= 120° + 120°

= 240°

11). m(arc CD) = 127° [Given]

m(arc AB) = 51° [Given]

m(arc AC) = m(arc BD) [Given]

m(arc CD) + m(arc BD) + m(arc AB) + m(arc AC) = 360°

127° + 2[m(arc BD)] + 51° = 360°

178° + 2[m(arc BD)] = 360°

2[m(arc BD)] = 360° - 178°

m(arc BD) = 91°

Since, m(arc CDB) = m(arc CD) + m(arc BD)

Therefore, m(arc CDB) = 127°+ 91°

= 218°

12). m(arc EH) + m(arc ED) + m(arc DH) = 360°

180° + 53° + m(arc DH) =360°

m(arc DH) = 360° - 233°

m(arc DH) = 127°