Question

Calculate the length of sides triangle pqr and determine weather or not triangle is a right angled. P(-4,6) q(6,1) r(2,9)

Answer 1

`\bold{\huge{\underline{ Solution }}}`

Given :-

• We have given the coordinates of the triangle PQR that is P(-4,6) , Q(6,1) and R(2,9)

To Find :-

• We have to calculate the length of the sides of given triangle and also we have to determine whether it is right angled triangle or not

Let's Begin :-

Here, we have

• Coordinates of P =( x1 = -4 , y1 = 6)
• Coordinates of Q = ( x2 = 6 , y2 = 1 )
• Coordinates of R = ( x3 = 2 , y3 = 9 )

By using distance formula

`\pink{\bigstar}\boxed{\sf{Distance=√((x_1-x_2)^2+(y_1-y_2)^2\;)}}`

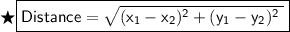
Subsitute the required values in the above formula :-

Length of side PQ

`\sf{ = }{\sf\sqrt{ (6 - (-4))^(2) + (1 - 6)^(2)}}`

`\sf{ = }{\sf\sqrt{ (6 + 4 )^(2) + (- 5)^(2)}}`

`\sf{ = }{\sf\sqrt{ (10)^(2) + (- 5)^(2)}}`

`\sf{ = }{\sf√( 100 + 25 )}`

`\sf{ = }{\sf√( 125 )}`

`\sf{ = 5 }{\sf√( 5 )}`

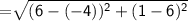
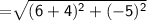
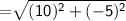
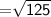
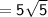
Length of QR

`\sf{ = }{\sf\sqrt{(2 - 6)^(2) + (9 - 1)^(2)}}`

`\sf{ = }{\sf\sqrt{(- 4 )^(2) + (8)^(2)}}`

`\sf{ = }{\sf√(16 + 64 )}`

`\sf{ = }{\sf√(80 )}`

`\sf{ = 4 }{\sf√(5 )}`

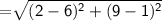
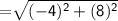
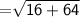
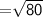
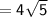
Length of RP

`\sf{ = }{\sf\sqrt{ (-4 - 2 )^(2) + (6 - 9)^(2)}}`

`\sf{ = }{\sf\sqrt{ (-6 )^(2) + (-3)^(2)}}`

`\sf{ = }{\sf√( 36 + 9 )}`

`\sf{ = }{\sf√( 45 )}`

`\sf{ = 3}{\sf√( 5 )}`

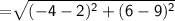
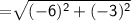
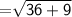
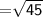
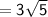
Now,

We have to determine whether the triangle PQR is right angled triangle

Therefore,

By using Pythagoras theorem :-

• Pythagoras theorem states that the sum of squares of two sides that is sum of squares of 2 smaller sides of triangle is equal to the square of hypotenuse that is square of longest side of triangle

That is,

`\bold{ PQ^(2) + QR^(2) = PR^(2)}`

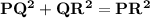
Subsitute the required values,

`\bold{ 125 + 80 = 45 }`

`\bold{ 205 = 45 }`

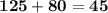
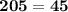
From above we can conclude that,

• The triangle PQR is not a right angled triangle because 205 ≠ 45 .