Question

Two loudspeakers in a plane are 2.0 m apart and in phase with each other. Both emit 700 Hz sound waves into a room where the speed of sound is 341 m/s. A listener stands 5.0 m in front of the loudspeakers and 2.0 m to one side of the center line. Is the interference at this point completely constructive, completely destructive, or in between

Answer 1

interference is between destructive and constructive

Step-by-step explanation:

The interference of two sound waves periodicity in phase by the speakers is

Δr =
`(\phi )/(2\pi ) \ \lambda`

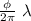
in this case they indicate that the frequency is f = 700 Hz, the wave speed is

v =λ f

λ = v / f

λ = 341/700

λ = 0.487 m

Let's use the Pythagorean theorem to find the distance that each wave travels

r₁ =
`√(x^2 + y^2)`

let's measure the distance from speaker 1

r₁ =
`√(5^2 + 1^2)`

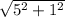
r₁ = 5,099 m

the distance from the second speaker

r₂ = \sqrt{x^2 + y^2}

r₂ =
`√(5^2 +3^2)`

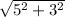
r₂= 5.831 m

the difference in the way is

Δr = r₂ -r₁

Δr = 5,831 - 5,099

Δr = 0.732 m

`( \phi )/(2\pi )` = Δr /λ

\frac{ \phi }{2\pi } = 0.732 / 0.487

\frac{ \phi }{2\pi } = 1.50

this is the phase difference this phase difference is approximately

Ф=
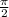`(\pi )/(2)` =1.57,

so the interference is between destructive ( Ф = π) and constructive (Ф=2π)