Question

The increasing annual cost (including tuition, room, board, books and fees) to attend college ) to attend college has been widely discussed in many publications including Money magazine. The following random samples show the annual cost of attending private and public colleges. Data are in thousands of dollars.

Private Colleges
53.8 42.2 44.0 34.3 44.0
31.6 45.8 38.8 50.5 42.0

Public Colleges
20.3 22.0 28.2 15.6 24.1 28.5
22.8 25.8 18.5 25.6 14.4 21.8

Required:
a. Compute the sample mean (in thousand dollars) and sample standard deviation (in thousand dollars) for private colleges.
b. What is the point estimate (in thousand dollars) of the difference between the two population means?

Answer 1

a) The sample mean is of 42.7 thousand dollars.

The standard deviation is of 6.38 thousand dollars.

b) The point estimate of the difference between the two population means is of 20.4 thousand dollars.

Explanation:

a. Compute the sample mean (in thousand dollars) and sample standard deviation (in thousand dollars) for private colleges.

Sample mean is the sum of all values divided by the number of values. So

`M = (53.8 + 42.2 + 44.0 + 34.3 + 44.0 + 31.6 + 45.8 + 38.8 + 50.5 + 42.0)/(10) = 42.7`

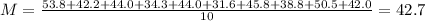
The sample mean is of 42.7 thousand dollars.

Sample standard deviation is the square root of the sum of the difference squared between each number and the mean, divided by the number of values. So

The standard deviation is of 6.38 thousand dollars.

b. What is the point estimate (in thousand dollars) of the difference between the two population means?

First, we have to find the sample mean for public colleges, and then subtract the sample mean of private colleges by the sample mean of public colleges. So, for public colleges:

`M = (20.3 + 22.0 + 28.2 + 15.6 + 24.1 + 28.5 + 22.8 + 25.8 + 18.5 + 25.6 + 14.4 + 21.8)/(12) = 22.3`

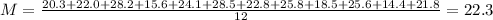
Point estimate of the difference:

42.7 - 22.3 = 20.4

The point estimate of the difference between the two population means is of 20.4 thousand dollars.