
Given :-
- We have given the coordinates of the triangle PQR that is P(-4,6) , Q(6,1) and R(2,9)
To Find :-
- We have to calculate the length of the sides of given triangle and also we have to determine whether it is right angled triangle or not
Let's Begin :-
Here, we have
- Coordinates of P =( x1 = -4 , y1 = 6)
- Coordinates of Q = ( x2 = 6 , y2 = 1 )
- Coordinates of R = ( x3 = 2 , y3 = 9 )
By using distance formula
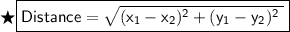
Subsitute the required values in the above formula :-
Length of side PQ
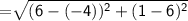
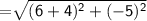
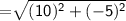
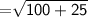
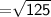
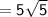
Length of QR
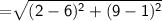
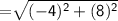
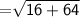
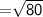
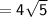
Length of RP
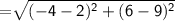
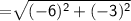
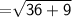
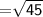
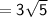
Now,
We have to determine whether the triangle PQR is right angled triangle
Therefore,
By using Pythagoras theorem :-
- Pythagoras theorem states that the sum of squares of two sides that is sum of squares of 2 smaller sides of triangle is equal to the square of hypotenuse that is square of longest side of triangle
That is,
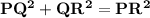
Subsitute the required values,
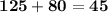
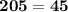
From above we can conclude that,
- The triangle PQR is not a right angled triangle because 205 ≠ 45 .