The error is when she added 4 to both sides.
Instead, she should divide both sides by -4 to undo the multiplication. Specifically, the multiplication between the -4 term and the (x-2)^2 term.
This is one possible correction of what her steps could look like.
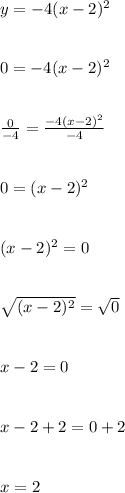
In the third step, I'm dividing both sides by -4. In the sixth step, I'm applying the square root to both sides to undo the squaring operation. Then two steps later, I'm adding 2 to both sides to undo the "-2", which helps fully isolate x.
The only solution is x = 2, so it's the only x intercept. You can verify this answer by plugging x = 2 back into the original equation at the very top. You should end up with y = 0.
Note: The term "root" is another name for "x intercept".