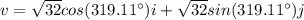Answer:
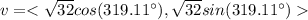 or
or
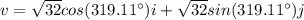
Explanation:
Find the magnitude of
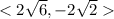 :
:
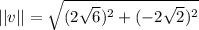
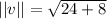
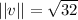
Find the direction angle of
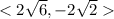 :
:
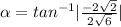
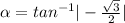
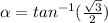
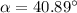
Since
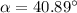 is our reference angle, we determine our direction angle
is our reference angle, we determine our direction angle
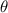 by verifying our angle is in Quadrant IV, which is where the vector is located. Therefore,
by verifying our angle is in Quadrant IV, which is where the vector is located. Therefore,
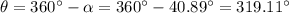
To represent a vector's magnitude and direction in trigonometric form, we use the form
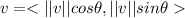 or
or
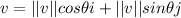 .
.
In conclusion, the trigonometric form of the vector is:
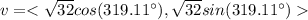 or
or