Question

R-134a is contained in a frictionless piston-cylinder device. The initial temperaure of the mixture is 39.37 oC. Over an hour 400 kJ of thermal energy is transferred to the roon which is maintained at a constant temperature of 22 oC. The condensation process is internally reversible. Determine the total entropy generation during this thermal energy process

Answer 1

Given :

Initial temperature of the refrigerant is :

`$T_i=39.37 ^ \circ C$`

= ( 39.37 + 273 ) K

= 312.3 K

Room which is maintained at constant temperature is :

`$T_o=22 ^ \circ C$`

= (22+273) K

= 295 K

The thermal energy transferred to the room is :

Q = 400 kJ

=
`$400 * 10^3 \ J$`

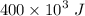
Therefore, the total entropy generation during the thermal energy process is :

`$\Delta S =\left[(-Q)/(T_i)+ (+Q)/(T_i)\right]$`

Here, -Q = heat is leaving the system maintained at a temperature of
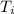`$T_i$` K.

+Q = heat is entering the system maintained at a temperature of
`$T_o$` K.

Therefore, substituting the values :

`$\Delta S =\left[(-400* 10^3)/(312.3)+ (400* 10^3)/(295)\right]$`

= [-1280.8197 + 1355.9322]

= 75.1125 J/K

= 0.0751125 kJ/K

= 0.075 kJ/K