Question

What can be the maximum value of the original kinetic energy of disk AA so as not to exceed the maximum allowed value of the thermal energy

Answer 1

The question is incomplete. The complete question is :

In your job as a mechanical engineer you are designing a flywheel and clutch-plate system. Disk A is made of a lighter material than disk B, and the moment of inertia of disk A about the shaft is one-third that of disk B. The moment of inertia of the shaft is negligible. With the clutch disconnected, A is brought up to an angular speed ?0; B is initially at rest. The accelerating torque is then removed from A, and A is coupled to B. (Ignore bearing friction.) The design specifications allow for a maximum of 2300 J of thermal energy to be developed when the connection is made. What can be the maximum value of the original kinetic energy of disk A so as not to exceed the maximum allowed value of the thermal energy?

Solution :

Let M.I. of disk A =
`$I_0$`

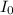
So, M.I. of disk B =
`$3I_0$`

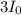
Angular velocity of A =
`$\omega_0$`

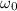
So the kinetic energy of the disk A =
`$(1)/(2)I_0\omega^2$`

After coupling, the angular velocity of both the disks will be equal to ω.

Angular momentum will be conserved.

So,

`$I_0\omega_0 = I_0 \omega + 3I_0 \omega$`

`$I_0\omega_0 = 4I_0 \omega$`

`$\omega = (\omega_0)/(4)$`

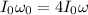
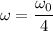
Now,

`$K.E. = (1)/(2)I_0\omega^2+ (1)/(2)3I_0\omega^2$`

`$K.E. = (1)/(2)I_0(\omega_0^2)/(16)+ (1)/(2)3I_0(\omega_0^2)/(16)$`

`$K.E. = (1)/(2)I_0\omega_0^2 \left((1)/(16)+(3)/(16)\right)$`

`$K.E. = (1)/(2)I_0\omega_0^2* (1)/(4)$`

`$\Delta K = (1)/(2)I_0\omega_0^2 - (1)/(2)I_0\omega_0^2 * (1)/(4) $`

`$2300=(3)/(4)\left((1)/(2)I_0\omega_0^2\right)$`

`$(1)/(2)I_0\omega_0^2=2300 * (4)/(3 ) \ J $`

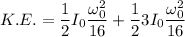
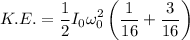
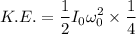
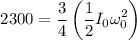
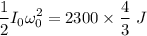
Therefore, the maximum initial K.E. = 3066.67 J