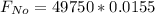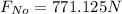Answer:
![(a)\ F_(No) = [P_(No) - (P_(area))/(2)]* A](https://img.qammunity.org/2022/formulas/physics/college/c6xyes2thp8wdad45eer28glk2fh2ai0am.png)
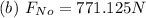
Step-by-step explanation:
Given
 ---- Altitude of container in Denver
---- Altitude of container in Denver
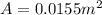 -- Surface Area of the container lid
-- Surface Area of the container lid
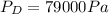 --- Air pressure in Denver
--- Air pressure in Denver
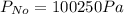 --- Air pressure in New Orleans
--- Air pressure in New Orleans
See comment for complete question
Solving (a): The expression for
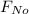
Force is calculated as:

The force in New Orleans is:
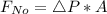
Since the inside pressure is half the pressure at sea level, then:
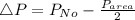
Where
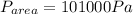 --- Standard Pressure
--- Standard Pressure
Recall that:
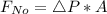
This gives:
![F_(No) = [P_(No) - (P_(area))/(2)]* A](https://img.qammunity.org/2022/formulas/physics/college/c1vefyg7gxj86nu4cvzts364whuhsvjtdn.png)
Solving (b): The value of
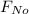
In (a), we have:
![F_(No) = [P_(No) - (P_(area))/(2)]* A](https://img.qammunity.org/2022/formulas/physics/college/c1vefyg7gxj86nu4cvzts364whuhsvjtdn.png)
Where
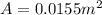
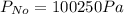
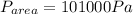
So, we have:
![F_(No) = [100250 - (101000)/(2)] * 0.0155](https://img.qammunity.org/2022/formulas/physics/college/yyxkx5mpdag0skl0c7xdx2i4aa2m4sng5q.png)
![F_(No) = [100250 - 50500] * 0.0155](https://img.qammunity.org/2022/formulas/physics/college/5rkwxusnq9si7qkmsn0mzj0fxgxflkwf0q.png)