Answer:
The correct option is -
Yes, because the Expected value is 1 and not negative which would imply that there is a chance of winning.
Explanation:
Given - A bag contains 10 blue marbles, 3 yellow marbles, and 12 orange marbles. If a blue marble is drawn you win $10. If a yellow marble is drawn you win $15. if an orange marble is drawn you lose $10. it cost $1 to play.
To find - Should you play the game?
Formula used -
Expected value , E[x] = ∑x p(x)
where p(x) is the probability.
Proof -
Given that,
Total blue marbles in a bag = 10
Total yellow marbles in a bag = 3
Total orange marbles in a bag = 12
So,
Total number of marbles in a bag = 10 + 3 + 12 = 25
Now,
Probability of getting blue marble =

Probability of getting yellow marble =
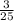
Probability of getting orange marble =
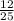
So,
Expected value , E[x] = ∑x p(x)
= (10)(
 ) + (15)(
) + (15)(
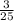 ) + (-10)(
) + (-10)(
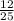 )
)
=

=

=
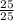
= 1
So,
Expected value = 1
So,
The correct option is -
Yes, because the Expected value is 1 and not negative which would imply that there is a chance of winning.