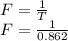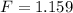Question

Two blocks are connected by a massless rope that passes over a 1 kg pulley with a radius of 12 cm. The rope moves over the pulley without slipping. The mass of block A is 2.1 kg and the mass of block B is 4.1 kg. Block A is also connected to a horizontally-mounted spring with a spring constant of 358 J/m2. What is the angular frequency (in rad/s) of oscillations of this system

Answer 1

`F=1.159`

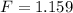
Step-by-step explanation:

From the question we are told that:

Mass of pulley
`M=1kg`

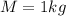
Radius
`r=12cm`

Mass of block A
`M_a=2.1kg`

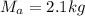
Mass of block B
`m_b=4.1kg`

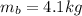
Spring constant
`\mu= 358 J/m2`

Generally the equation for Torque is mathematically given by

Since
`\sumF=ma`

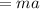
At mass A

`T_2-f_3=2.1a`

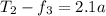
At mass B

`4.8-T_1=4.1a`

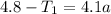
At Pulley

`R(T_1-T_2)=(1*1*R^2)/(2)(a)/(R)`

`R(T_1-T_2)=0.55a`

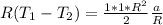
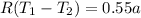
Therefore the equation for total force F

At mass A+At mass B+At Pulley

`(T_2-f_3+4.8-T_1+R(T_1-T_2)=2.1a+4.1a+0.55a`

`(T_2-f_3+4.8-T_1+R(T_1-T_2)=2.7a+4.8a+0.55a`

`-f_3+4.1=6.75a`

`-f_3=6.75a+4.8`

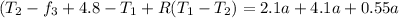
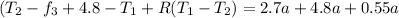
Since From above equation

`M_(eff)=6.7kg`

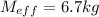
Therefore

`T=2\pi \sqrt{{(M_(eff))/(k)}`

`T=2\pi \sqrt{{(6.75)/(\mu)}`

`T=0.862s`

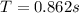
Generally the equation for frequency is mathematically given by

`F=(1)/(T) \\F=(1)/(0.862)`

`F=1.159`