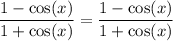Question

asked Aug 21, 2022 152k views

1 Answer

Followben · Answer 1 · 2022-08-28T17:43:01+0000

Answer:

See Below.

Explanation:

Problem 1)

We want to verify that:

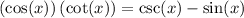
$\displaystyle \left(\cos(x)\right)\left(\cot(x)\right)=\csc(x)-\sin(x)$

Note that cot(x) = cos(x) / sin(x). Hence:

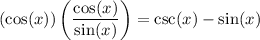
$\displaystyle \left(\cos(x)\right)\left((\cos(x))/(\sin(x))\right)=\csc(x)-\sin(x)$

Multiply:

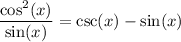
$\displaystyle (\cos^2(x))/(\sin(x))=\csc(x)-\sin(x)$

Recall that Pythagorean Identity: sin²(x) + cos²(x) = 1 or cos²(x) = 1 - sin²(x). Substitute:

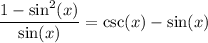
$\displaystyle (1-\sin^2(x))/(\sin(x))=\csc(x)-\sin(x)$

Split:

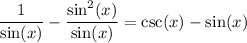
$\displaystyle (1)/(\sin(x))-(\sin^2(x))/(\sin(x))=\csc(x)-\sin(x)$

Simplify:

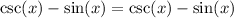
$\csc(x)-\sin(x)=\csc(x)-\sin(x)$

Problem 2)

We want to verify that:

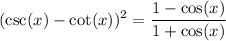
$\displaystyle (\csc(x)-\cot(x))^2=(1-\cos(x))/(1+\cos(x))$

Square:

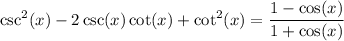
$\displaystyle \csc^2(x)-2\csc(x)\cot(x)+\cot^2(x)=(1-\cos(x))/(1+\cos(x))$

Convert csc(x) to 1 / sin(x) and cot(x) to cos(x) / sin(x). Thus:

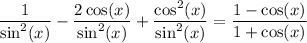
$\displaystyle (1)/(\sin^2(x))-(2\cos(x))/(\sin^2(x))+(\cos^2(x))/(\sin^2(x))=(1-\cos(x))/(1+\cos(x))$

Factor out the sin²(x) from the denominator:

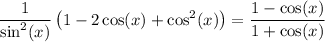
$\displaystyle (1)/(\sin^2(x))\left(1-2\cos(x)+\cos^2(x)\right)=(1-\cos(x))/(1+\cos(x))$

Factor (perfect square trinomial):

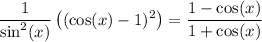
$\displaystyle (1)/(\sin^2(x))\left((\cos(x)-1)^2\right)=(1-\cos(x))/(1+\cos(x))$

Using the Pythagorean Identity, we know that sin²(x) = 1 - cos²(x). Hence:

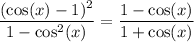
$\displaystyle ((\cos(x)-1)^2)/(1-\cos^2(x))=(1-\cos(x))/(1+\cos(x))$

Factor (difference of two squares):

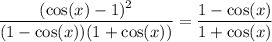
$\displaystyle ((\cos(x)-1)^2)/((1-\cos(x))(1+\cos(x)))=(1-\cos(x))/(1+\cos(x))$

Factor out a negative from the first factor in the denominator:

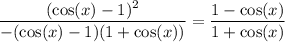
$\displaystyle ((\cos(x)-1)^2)/(-(\cos(x)-1)(1+\cos(x)))=(1-\cos(x))/(1+\cos(x))$

Cancel:

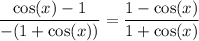
$\displaystyle (\cos(x)-1)/(-(1+\cos(x)))=(1-\cos(x))/(1+\cos(x))$

Distribute the negative into the numerator. Therefore:

$\displaystyle (1-\cos(x))/(1+\cos(x))=\displaystyle (1-\cos(x))/(1+\cos(x))$

Please log in or register to add a comment.