Solution :
a).
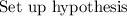
 : There is no significance between them.
: There is no significance between them.
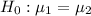
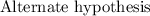 : There is significance between them.
: There is significance between them.
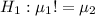
b). Test statics

Standard deviation
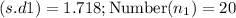
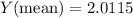
Standard deviation
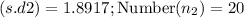
We use the test statics :
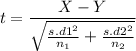
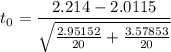
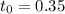

c. The critical value of |t| with minimum
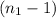 , i.e. 19 d.f is
, i.e. 19 d.f is
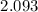
We got
 = 0.35439 and |t| = 2.093
= 0.35439 and |t| = 2.093