Question

Arrivals of cars at a gas station follow a Poisson distribution. During a given 5-minute period, one car arrived at the station. Find the probability that it arrived during the last 30 seconds of the 5-minute period g.

Answer 1

0.9 = 90% probability that it arrived during the last 30 seconds of the 5-minute period.

Explanation:

The car is equally as likely to arrive during each second of the interval, which means that the uniform distribution is used to solve this question.

A distribution is called uniform if each outcome has the same probability of happening.

The uniform distribution has two bounds, a and b, and the probability of finding a value higher than x is given by:

`P(X \geq x) = (b - x)/(b - a)`

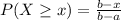
5-minute period

This means that
`a = 0, b = 5*60 = 300`

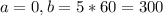
Find the probability that it arrived during the last 30 seconds of the 5-minute period.

300 - 30 = 270. So

`P(X \geq 270) = (300 - 270)/(300 - 0) = 0.9`

0.9 = 90% probability that it arrived during the last 30 seconds of the 5-minute period.