Question

IV. An annealed copper strip 9 inches wide and 2.2 inches thick, is rolled to its maximum possible draft in one pass. The following properties of annealed copper are given: strength coefficient is 90,000 psi; true strain at the onset of non-uniform deformation is 0.45; and, engineering strain at yield is 0.11. The coefficient of friction between strip and roll is 0.2. The roll radius is 14inches and the rolls rotate at 150 rpm. Calculate the roll-strip contact length. Calculate the absolute value of thetrue strain that the strip undergoes in this operation. Determine the average true stress of the strip in theroll gap. Calculate the roll force. Calculate the horsepower required.

Answer 1

13.9357 horse power

Step-by-step explanation:

Annealed copper

Given :

Width, b = 9 inches

Thickness,
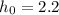`$h_0=2.2$` inches

K= 90,000 Psi

μ = 0.2, R = 14 inches, N = 150 rpm

For the maximum possible draft in one pass,

`$\Delta h = H_0-h_f=\mu^2R$`

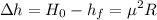
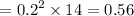`$=0.2^2 * 14 = 0.56$` inches

`$h_f = 2.2 - 0.56$`

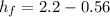
= 1.64 inches

Roll strip contact length (L) =
`$√(R(h_0-h_f))$`

`$=√(14 * 0.56)$`

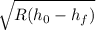
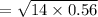
= 2.8 inches

Absolute value of true strain,
`$\epsilon_T$`

`$\epsilon_T=\ln \left((2.2)/(1.64)\right) = 0.2937$`

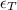
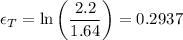
Average true stress,
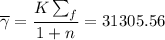`$\overline{\gamma}=(K\sum_f)/(1+n)= 31305.56$` Psi

Roll force,
`$L * b * \overline{\gamma} = 2.8 * 9 * 31305.56$`

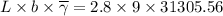
= 788,900 lb

For SI units,

Power =
`$(2 \pi FLN)/(60)$`

`$=(2 \pi 788900* 2.8* 150)/(60* 44.25* 12)$`

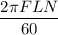
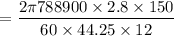
= 10399.81168 W

Horse power = 13.9357