Answer:
A
Explanation:
We are given the function:
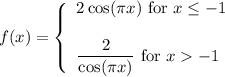
And we want to find:
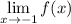
So, we need to determine whether or not the limit exists. In other words, we will find the two one-sided limits.
Left-Hand Limit:
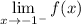
Since we are approaching from the left, we will use the first equation:
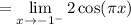
By direct substitution:
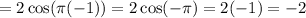
Right-Hand Limit:
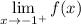
Since we are approaching from the right, we will use the second equation:
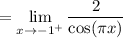
Direct substitution:
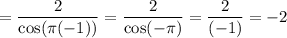
So, we can see that:
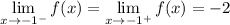
Since both the left- and right-hand limits exist and equal the same thing, we can conclude that:
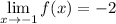
Our answer is A.